Tema: Teorema límites

Con las explicaciones que nos presentó el profeso comprendí que si los resultados del problema da fracción de ceros (0/0) es porque se debe de resolver de una forma diferente, ya que el valor está escondido en el mismo problema por lo que se realiza factorización para poder resolver el problema. También aprendí que los resultados no pueden dar decimales, solo terminan en fracción o en números enteros pueden ser negativos o positivos.

Los teoremas sobre los límites son las proposiciones de cómo se comportan los limites en ciertas operaciones de manera general y que nos ayudan a resolver problemas más complejos:

Limites indeterminados, La indeterminación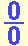

Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.

Ejemplo. Halle

Al sustituir, resulta y lo que genera una indeterminación del tipo .

Sin embargo, como si x ¹ 3, resulta que la función coincide con la función (x + 3) salvo en x = 3.

Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el comportamiento de analizando el de la función (x + 3).

Por lo tanto puede decirse que